Link to GitHub
Hi Tino,
You mention in the video that the t’s have to be “above 2” and the probabilities “nice and small”, what would we do if that is not the case … Any advice where/how I could read more or how to tackle this?
Hi Eddy,
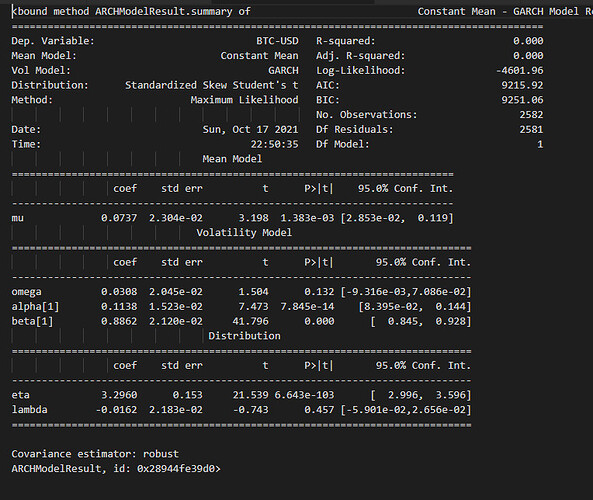
It’s just a rule of thumb, but not the law. My main concern is using GARCH which it’s not the right tool for the job.
BTC-USD is very unlikely to exhibit GARCH properties, and BTC is unlikely to follow any parametric distribution. It’s a VERY hard asset class to simulate.
My recommendation is to bootstrap the returns: Take all the daily returns for the past 5 years, write that number on a little piece of paper and put it in a bag. Then pick one of the pieces of paper and make that your day 1 return, rinse and repeat a thousand time and you have a new simulated time series, with values that came from the original population.
I don’t think what you are trying to achieve is possible with GARCH, or any other nice parametric model.
Let me know how you go!
Cheers,
Tino
Hi Tino,
Thank you for the video, I have a problem to solve. I have to generate some time series with a given standard deviation and a given mean for each year. Also the series should be no negative and the sum of them should be equal to an amount. How could I simulate them? Could be possible with GARCH model showed above? How can I guarantee that the sum is equal to a particular amount keeping the means and the SD for each year?
Hi Fed, welcome onboard.
That would be pretty easy if you just want homoskedastic variance:
import numpy as np
import pandas as pd
year_mean = 0.001
daily_mean = year_mean /250
yearly_std = 0.20
daily_std = yearly_std /16
days_to_simulate = 1000
rets = pd.DataFrame(np.random.normal(daily_mean, daily_std , days_to_simulate ), columns = ['Sim Rets'])
prices = 100*(1+rets).cumprod()-1
Now the question comes, do you want GARCH effects in the returns, or are you happy with something simple like the above?
It’s sort of tricky to have a certain vol in mind and then say I want to back into GARCH. Also, I guess we are using sample std as the measuring stick?
What I would suggest is to generate some GARCH simulated returns as per the video/notebook, and then scale them up/down to your target vol.
Simply a case of dividing and multiplying the whole series until the std of the prices matches what you want.
Also, because we are doing % returns of a price, it will never be negative.
Not sure what you mean around the sum being equal to a certain amount?
Cheers,
Tino
Hi Tino, thank you for your answer,
I give you an example so is easier to explain what I mean.
I have a vector of means X=(x1,x2,…,xn), in n years (14 years real data, I do not have days), These means are different. I also have the coeff of variation so given X I have the standard deviations SD for each year. Now Y=x1+x2+…+xn and Y=a where a is a constant and is given.
In a different point of view, I would like to model the contributions in private equity where the sum of them (Y) should be equal to the commitment (a) so we can also look at that as a drawdown of the cumulative non contributed capital.
I want to generate a lot of time series with the conditions above. So I would like for example at time 1 the mean of those paths at time 1 that is equal to x1 and SD equal to SD1. At time 2 I want the mean of the samples at time 2 equal to x2 with SD2 and so on. In the end I want that each of these paths is equal to a constant a. Of course, each of them should have no negative numbers.
I believe that an homoskedastic model could fit because the Coff of variation is constant during the time but the means are different so I am not totally sure if is the right way because the means change and maybe would be easier model it during the time.
I also give you a paper if you want,
Paper: Modeling the Cash Flow Dynamics of Private Equity Funds –Theory and Empirical Evidence
Authors: Axel Buchner, Christoph Kaserer and Niklas Wagner
The problem of this paper is that they do not assume the sum si equal to a but just the contribution would never be higher than the commitment (with exponential decay process). So, I just assumed that the last sample would be equal to the sum of the previous contributions at every time, and it looks good. The problem is that I do not have control of means, if I compute the means in each year, I have a huge error compared to the real means, so I am exploring other models or other way to reach the result. Do you have any ideas how to reach this result?
Hi Fed,
I think all you need to do is keep changing the mean and std for each of the years and then stick them all together.
Cheers,
Tino